
The original article can be find here: Morphologically Adaptive Crash Landing on a Wall: Soft‐Bodied Models of Gliding Geckos with Varying Material Stiffnesses – Chellapurath – 2022 – Advanced Intelligent Systems – Wiley Online Library
The original article as a pdf: Advanced-Intelligent-Systems-2022-Chellapurath.pdf
Landing on vertical surfaces in challenging environments is a critical ability for multimodal robots—it allows the robot to hold position above the ground without expending energy to hover. Asian flat-tailed geckos (Hemidactylus platyurus) are observed to glide and perch on vertical surfaces by relying on their tail and body morphology, potentially reducing the control effort to perch. This novel perching mechanism using a bioinspired physical model is discussed and its tail and body parameters to determine their influence on perching success and the kinematics of the gecko’s dynamic landing maneuver are adjusted. Perching performance is evaluated by changing the model’s torso and tail stiffness. Combining a compliant torso and stiff tail enables the model to passively perch on a vertical substrate with a success rate >90%, compared with ≈10% without a tail attached. A compliant torso is necessary to absorb the in-flight kinetic energy and accommodate the uncertainties in approach conditions. Similar to the gecko’s perching strategy, the stiff tail pushes against the substrate, preventing the model from falling backward head over heels. These findings highlight the critical role of tail and material stiffness for perching and provide a simplified mechanism to impart perching capabilities in robots.
1 Introduction
Studies invoking biomitetics have gained significant popularity over the last two decades, allowing for the construction of more lifelike robots inspired by nature. The goal of bioinspired robotics is often twofold: understanding nature’s fundamental processes and acquiring the capacity to replicate those processes to ultimately construct improved robotic platforms with similar capability. By examining the underlying principles of locomotion strategies found in nature, researchers sought to develop robots with similar capabilities in aerial,[1, 2] aquatic,[3–8] and terrestrial[9–12] environments as well as using the robots as platforms in biomechanics research to understand the fundamentals of animal locomotion.[13]
To negotiate compelx environments and flow regimes, animals must be able to perform multimodal locomotion. Highly maneuverable multimodal locomotion is needed for diverse survival needs such as fast escape from predators, quick pursuit, searching for food, breeding, nesting, preserving energy, and migration.[14] The most delicate aspect of multimodal locomotion is the challenging transition from one mode to another at the intersection land–air, water–air, or water–land. Flying and gliding animals transition from air to land by perching on a diverse range of complex, natural, and surfaces.[15] From large birds to microscopic insects, animals rely mostly on passive mechanisms to perch. Birds decelerate in the air utilizing their morphing wings and tail and then land slowly in a controlled fashion as they approach the substrate. During landing, they bend their legs, resulting in a tendon on the ankle’s backside to naturally force the toes to grip around a branch. This passively operated mechanism is critical for perching without active gripping control.[16, 17] Smaller animals also depend on the functional morphology to increase robustness and reduce neural control effort honeybees use the swinging motion of their abdomen to dissipate residual flying energy to achieve a smooth, stable, and quick landing.[18] Houseflies perch by using their compliant legs to dissipate the high kinetic energy of flight.[19]
Perching is not limited to flight animals. Gliding animals in the absence of thrust generation capabilities can also modify their body orientation and body shape to successfully perch.[20–23] Gliding mammals and flying lizards possess well-defined aerodynamic surfaces allowing them to significantly decelerate their descent and control their body orientation before perching.[24] Lizards can use their tails for mid-air righting reflexes as well as for turning during gliding as discovered by Ardian Jusufi and colleagues.[24, 25] By contrast, flying snakes and gliding geckos lack extensive aerodynamic surfaces and instead rely on their body and/or tail to successfully perch.[22, 26] These diverse mechanisms across flapping and gliding animals have inspired several perching mechanisms used in present-day aerial vehicles.
Aerial robots with perching capabilities can stabilize contacts with high structures to obtain force support, allowing the robots to depend less on the lift generated by the propellers and stay perform stationary holding with lesser control effort. As a result, perching extends the overall mission time and exploits a more extensive range of structures in the environment. Animals have been a source of inspiration for aerial robots[27] with perching capabilities, which is crucial for modern-day aerial vehicles to perform challenging tasks in complex natural environments like collecting ground-based data, performing inspection duties, or manipulating items.[28–35]
Among the complex natural and synthetic substrates, vertical surfaces are challenging among the candidate sites for perching, especially if the aerial vehicle or animal lacks extensive aerodynamic control surfaces. Incorporating aerodynamic control surfaces in aerial vehicles increases the cost of transport and the complexity of controlling those surfaces to enable perching. Surprisingly, gliding geckos (Hemidactylus platyurus) have evolved to successfully perch on vertical substrates even in the absence of extensive aerodynamic surfaces to decelerate themselves at the time of landing, simply relying on the adaptive stiffening of their compliant body parts on impact. Figure 1a shows the motion sequence of the gecko approaching the vertical target. First, it impacts the tree with the head and anterior torso with a positive angle of attack. After the impact, the body is rotated downward about the head, and the hind limbs anterior torso to the tree trunk. Due to high peak forces on impact the bounces off, with forelimbs slipping off, and the torso rotates with its back toward the forest floor as the tail pushes into the tree surface. The torso attains the maximum pitch back, and the animal momentarily comes to rest before its torso returns to the tree trunk so that the front legs regain a foothold. Siddall, Byrnes, Full, and Jusufi investigated the utility of tails for the fall arresting response (FAR) upon landing, employing a dynamic mathematical model and robotic physical model (Figure 1b,c).[36]
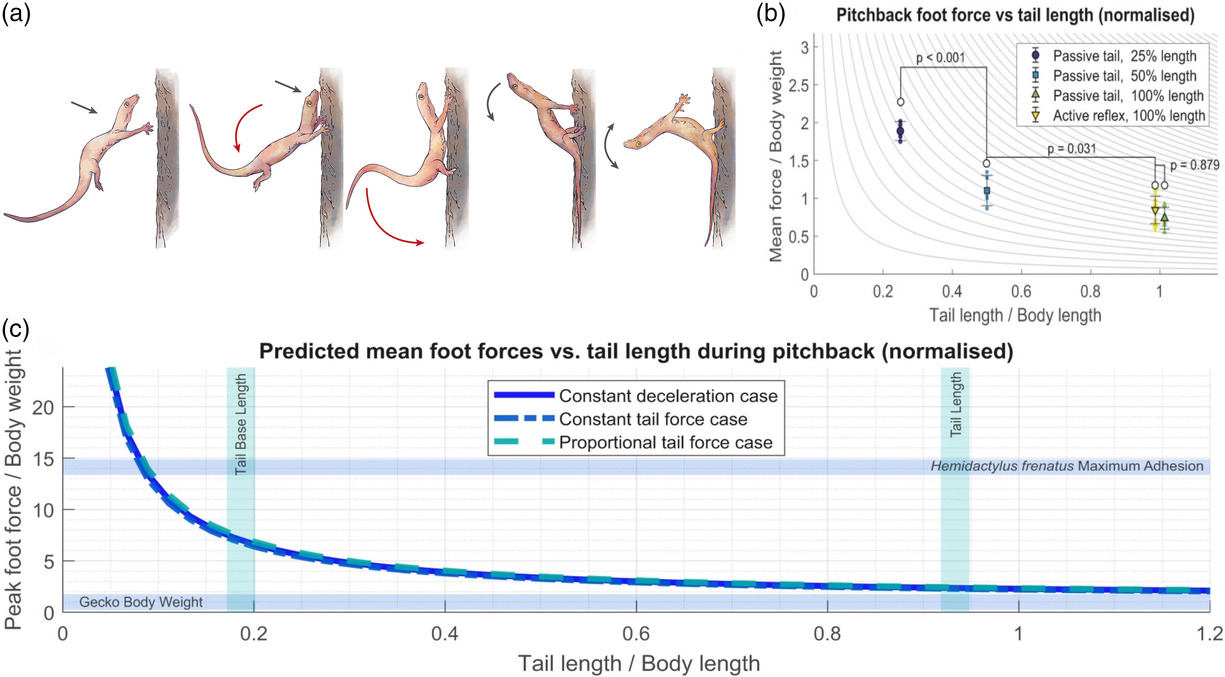
Figure 1
Apart from the presence or lack of a tail, various additional physical and geometrical parameters may play a role in the dynamics of perching, such as the tail’s stiffness and length, or stiffness of the torso. Investigating the effects of those characteristics on perching dynamics is critical for improving the perching capabilities of aerial vehicles and also for understanding the biology of perching in gliding animals. For instance, the influence of tail length and torso stiffness on perching capability may be related to the variation in body size and morphology of gliding animals in the wild, ultimately influencing their survival.
In this study, we analyze the tail-assisted FAR in the gliding Asian flat-tailed gecko (H. platyurus) using a simple passive robo-physical model.[37] The robo-physical model allows us to selectively change the tail length, as well as the stiffness of tail and torso separately. The model has weight and size dimensions that are similar to the gliding gecko species we discovered performing the FAR in the field.[36] We find that a decrease in tail length reduces the perching success rate in-line with the observation of tailless gliding geckos in the wild and our previous experimental robotics results.[36] We study the importance of physical and geometrical characteristics in the perching process, including tail length, tail stiffness, and torso stiffness. The findings of this work provide insight on the selective forces acting on the animal, which are highly complex to investigate in live animal trials. Furthermore, the results can drive the development of innovative perching mechanisms in robotics inspired by biological material and system relationships.
2 Results and Discussion
2.1 Design and Fabrication of Prototype
The physical prototype was fabricated in the dimensions of H. platyurus. The snout-vent length was 54 mm and the tail length was 50 mm. Small weights were added on to the foam so that the physical model had a mass distribution similar to that of gecko (80–90% torso and 10–20%[25]) as can be seen in Figure 2a,b. The base material of the prototype was flexible polyethylene (PE) foam (5 mm thick and 10 mm wide) and the stiffness of the torso and the tail were varied by adding thin flexible sheets of material with different Young’s modulus (E) at the lower surface of the body (Table 1). Stiffening materials included rubber tape, plastic sheet, and carbon fiber reinforced plastic (CFRP) plates. The legs were constructed using plastic sheets that were bent and thermoformed to make simple flexible joints that were light in weight. Velcro tapes affixed to the foot served as the adhesive material in this study.
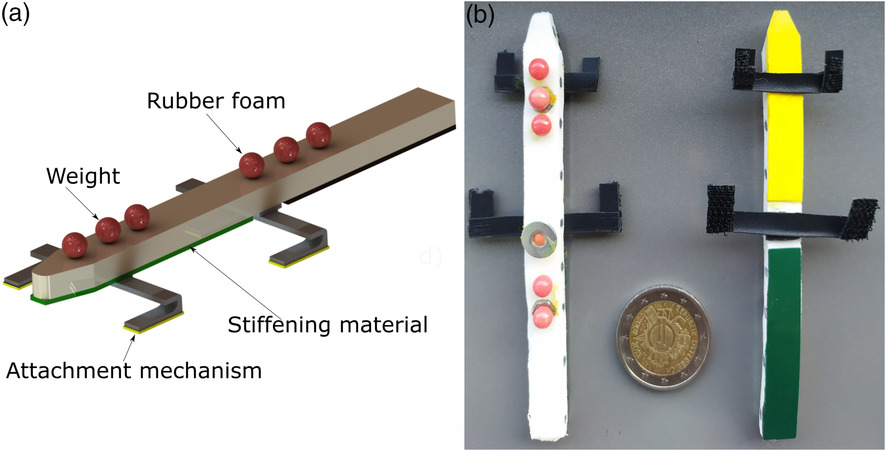
Figure 2
| Stiffness name | Base material | Stiffening material (SM) | Young’s modulus of SM [MPa] |
|---|---|---|---|
| S1 | PE foam | No stiffening material | 0.61 |
| S2 | Rubber tape | 23 | |
| S3 | Polyethylene sheet | 1240 | |
| S4 | CFRP plate | 70 000 |
2.2 Tail Stiffness and Length
We manufactured four prototypes with varying tail stiffnesses (Stail) to investigate the role of tail stiffness in the perching process: S1tail < S2tail < S3tail < S4tail as described in Section 4. All four prototypes of the physical prototype had a torso stiffness S1torso. The prototype with tail stiffness S1tail had a high failure rate due to the tail’s oscillation with the substrate after impact, which resulted in the tail being out of contact when the torso pitched back as shown in the Video S1, Supporting Information. With tail stiffness S1tail, the torso and the tail rebound simultaneously (Figure 3a), making it impossible for the hind limbs to remain connected to the wall due to the combined inertial forces of the torso and tail, resulting in the prototype falling off. However, with stiffer tails (S2tail, S3tail, and S4tail), the tail remained in contact with the surface during the pitch back of the torso, preventing the prototype from falling (Figure 3a), as the oscillation of their tail was damped faster than the low stiffness tail S1tail. Hence, the success rate of perching was higher for prototypes with tail stiffness S2tail, S3tail, and S4tail, compared to S1tail. The success rate with tail stiffness S1tail, S2tail, S3tail, and S4tail was 51.6% (N = 31), 93.5% (N = 31), 92.3% (N = 26), and 85.2% (N = 27), respectively (Figure 3b). The observation in Figure 3a was verified by examining the mean horizontal velocity fluctuation of the tail tip in each experimental set (Figure 3c). The tail with S2tail and S3tail was able to deform during the pitch back and hence absorb the energy during the rebound of the torso. However, the stiffest tail (S4tail) was not able to deform, and the energy absorption might have taken place mainly due to deformation in the joint at the beginning of the tail and this may be the reason for the slight decrease in the success rate with an increase in the tail stiffness from S2tail to S4tail (Figure 3b).
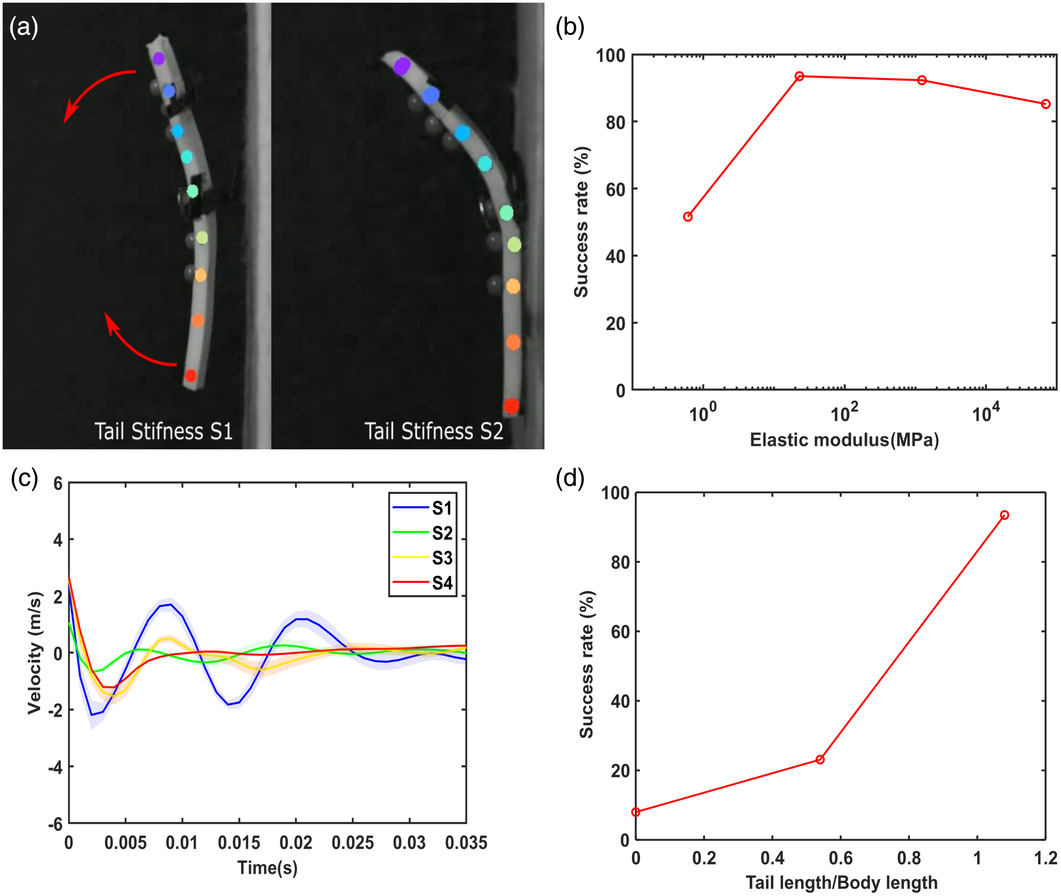
Figure 3
The results suggest that the tail stiffness is critical to achieving robust perching behavior (success rate > 80%); however, the perching outcome is consistent above a certain level of stiffness. If the tail is considered as a cantilever beam fixed at one end, the stiffness of the tail is defined as
where E is Young’s modulus, I is the second moment of area, and L is the length. The stiffness can be increased either by increasing the value of E and I or by decreasing the length of the tail. However, decreasing the length of the tail is counterproductive as the length of the tail has a positive proportional relationship with the success rate (Figure 3d). The success rate for 100%, 50%, and 0% tail lengths was 93.5% (N = 31), 23.1% (N = 26), and 8% (N = 25). The tail creates a counter torque during the pitch back of the gecko, reducing the force on the hind limbs. The tail stiffness and tail length results suggest that a long tail (tail length/body length ≥ 1) with high stiffness property (E) could produce a robust perching behavior.
The results suggest that the gecko may stiffen its tail when it hits the substrate to prevent it from rebounding. Moreover, a tapered tail in geckos could also help reduce the rebounding. In a tapered tail, the center of mass is more toward the base of the tail, resulting in a lower bending moment generated from the reaction force due to impact. The tapered tail also has a higher value of second moment of area closer to the base, helping the gecko arrest the rebound faster.
2.3 Torso Stiffness
The torso stiffness also plays a crucial role in the energy dissipation after the crash landing with the head. To understand the role of torso stiffness in the perching mechanism, we prepared prototypes with four different torso stiffnesses (S1torso < S2torso < S3torso < S4torso). The tail stiffness for all four prototypes was selected as S2tail owing to its high success rate in previous experiments. With stiffness S1torso after impact, the torso curved onto the vertical wall (Figure 4a), absorbing the energy due to the impact. Instead of bending onto the wall, the highly stiff torso (S3torso and S4torso) pivots about the head and impacts the wall with hind limbs and tail with high kinetic energy as shown in the supplementary video and Figure 4b. The amount of torso bending decreases with increasing stiffness, indicated by the value of minimum radius/snout-vent length of the torso as described in Section 4. The bending of the torso increases with an increase in torso stiffness (Figure 4c). The kinetic energy of hind limbs at the time of impact on the wall for different torso stiffnesses is shown in (Figure 4d). The kinetic energy of the hind limbs at impact increased with increasing torso stiffness, indicating the low stiffness torso absorbs more kinetic energy during the initial collision. Moreover, the bending of the torso helped to extend the time window of energy dissipation. Figure 4e shows the time duration from the initial impact with the collision of the head, to the impact of the hind limbs.
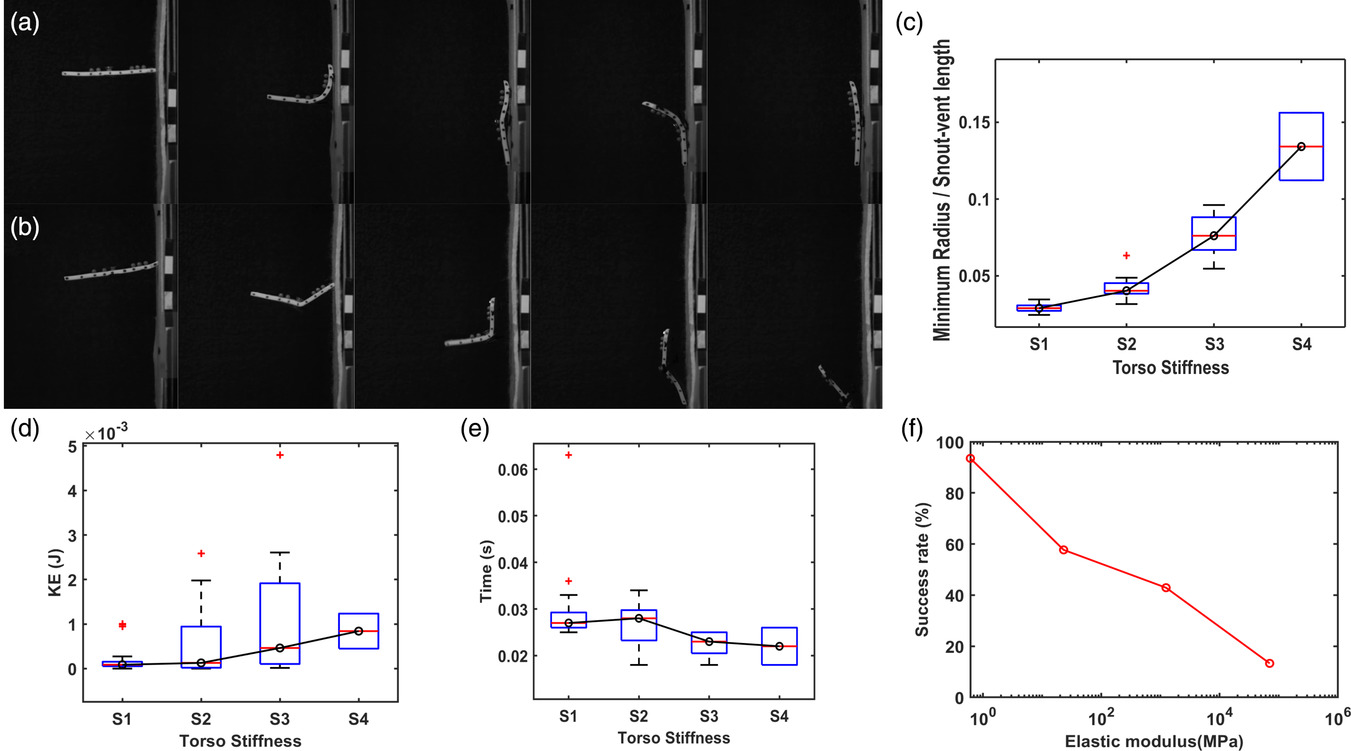
Figure 4
As a result of all these factors, the success rate decreased with increase in torso stiffness (Figure 4f). The success rate of prototypes with torso stiffness S1torso, S2torso, S3torso, and S4torso was 93.5% (N = 31), 57.7% (N = 26), 42.9% (N = 28), and 13.3% (N = 15), respectively.
The orientation of the prototype at impact also played an essential role in the success rate of perching. The prototype with torso stiffness S1torso was able to perch successfully even at high approach angles. However, the prototype with torso stiffness S2torso, S3torso, and S4torso failed to perch at steep approach angles. For example, at steep approach angles the prototype S3 bounced off the wall, in contrast to S1, which aligned successfully. As a result, the hind limbs were not able to attach to the substrate (Figure 4a,b) in S3.
Geckos do not have an aerodynamic control surface like birds to stall when approaching the tree. However, similar to the prototype, the compliance of their body might absorb the kinetic energy from the glide by performing a FAR on impact and perch successfully even with a high descent velocity.
These capabilities are essential for aerial and arboreal robots to perch on challenging vertical surfaces. If the robot has a passive perching mechanism, relying on the body’s morphology to absorb the landing impact energy, it avoids the need for any active damping system, helping the robot reduce the net weight and thus save energy during flight and facilitates cost-effective station holding.
2.4 Effect of Approach Kinematics
An important aspect influencing the perching capability is how the prototype approaches the vertical landing substrate. The orientation of the prototype at impact (�oi), the glide angle at impact (�gi), and the speed at impact can influence the perching dynamics and, ultimately, the perching success or failure. Furthermore, perching mechanisms need to be robust to variations in those factors to perch successfully in real-life conditions. We varied �oi and �gi to test the influence of each variable on the perching capability of the prototype. The speed at impact was not consistent across experimental groups and was significantly higher for S2tail and S3tail in the tail stiffness experiments and for S3torso and S4torso in the torso stiffness experiments. Significantly higher impact speeds across experimental groups can lead to an artificial correlation between impact speed and perching success. To avoid this artifact, the impact speed was considered a random effect in the regression analysis.
Across all experiments with different tail stiffnesses, the �o varied from −1.6° to 34.2° while the �gi varied between −50.4° and −58.6°. The speed at impact was 3.4 ± 0.2 m s−1 (N = 115). We used a generalized linear mixed-effects model with a binomial distribution for the response variable to investigate the correlation between prototype tail/torso stiffness, �oi, and �gi on perching success/failure. To account for the variation in impact speed across experimental groups, we included the impact speed as a random effect in the model. The regression model was
For tail stiffness, the model showed a significant positive correlation between tail stiffness and the outcome of success (Table 2). The glide angle and the orientation at impact were not significantly correlated, suggesting that the prototype was robust to variations in glide angle and orientation at impact. These results are consistent with the observation that a higher tail stiffness facilitates rapid damping postimpact leading to tail engagement at the time of pitch back of the torso (Figure 3b).
| Variable | Estimate | SE | 95% CIlower | 95% CIupper | t | p | SD (random effect) |
|---|---|---|---|---|---|---|---|
| (intercept) | 0.543 | 1.300 | −2.030 | 3.117 | 0.418 | 0.676 | 0.268 |
| Stiffness | 0.104 | 0.032 | 0.042 | 0.167 | 3.295 | 0.001* | |
| �oi | −0.007 | 0.004 | −0.015 | 0.001 | −1.652 | 0.101 | |
| �gi | −0.002 | 0.024 | −0.049 | 0.044 | −0.109 | 0.914 |
In the torso stiffness experimental groups, the �oi varied from −4.5° to 35.2° and the �gi varied between −45.2° and −58.1°. The speed at impact was 3.8 ± 0.3 m s−1 (N = 100). We used the regression model specified in Equation (2) to test the effect of torso stiffness, orientation at impact, glide angle at the impact on the perching success/failure of the prototype. The torso stiffness was negatively correlated with the perching success (Table 3). The regression results support the observation that a more compliant torso extends the window of energy dissipation at impact compared to a stiffer torso by bending; the minimum radius of curvature/snout-vent length for S1torso was 0.58 ± 0.06 (N = 29) which was significantly lower than S3torso at 1.53 ± 0.26 (N = 12) (Figure 4). Furthermore, an increase in pitch orientation at impact increased the perching success of the prototype; the orientation at impact was positively correlated with perching success (Table 3). A higher pitch orientation at impact is especially relevant in the case of a stiffer torso because a higher pitch orientation mitigates the requirement of torso bending to engage the hindlimbs and the tail with the substrate (Figure 5). However, if the torso is too stiff (S4torso), it can lead to a high rebounding of the prototype at impact leading to hind limbs not engaging with the substrate. This was observed most in the S4torso experimental setup, with only 2 out of 15 trials resulting in perching success.
| Variable | Estimate | SE | 95% CIlower | 95% CIupper | t | p | SD (random effect) |
|---|---|---|---|---|---|---|---|
| (intercept) | −2.482 | 8.502 | −19.363 | 14.398 | −0.292 | 0.771 | 0.165 |
| Stiffness | −1.240 | 0.345 | −1.924 | −0.555 | −3.596 | <0.001* | |
| �oi | 0.098 | 0.037 | 0.024 | 0.172 | 2.637 | 0.010 | |
| �gi | −0.181 | 0.140 | −0.458 | 0.096 | −1.295 | 0.198 |
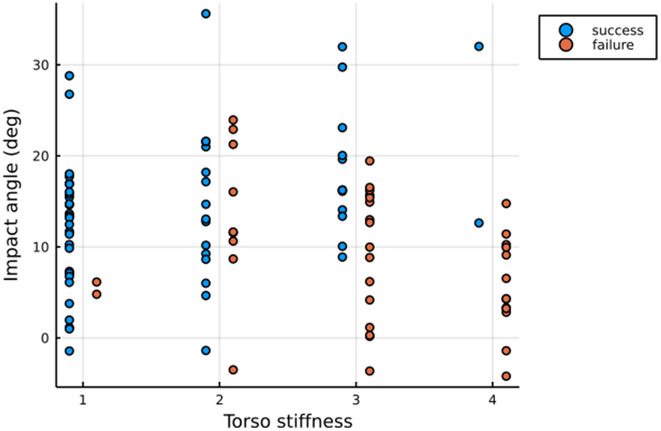
Figure 5
The approach kinematics can influence the perching dynamics. The amount of pitch back and the bending of the torso may depend on approach kinematics like the orientation at impact or glide angle. Our analysis shows that the maximum pitch back angle increases with a decrease in impact orientation, i.e., the prototype showed high torso bending at steep orientations on impact (Figure 6a). The prototype orientation at impact also played a role in the torso bending after the impact. The Rmin/lsv increased with increase in orientation of impact (Figure 6b). The Rmin/lsv also increased a higher torso stiffness. The glide angle was not correlated with the pitch back angle, and a moderate correlation with torso bending (r = 0.458, p < 0.001).
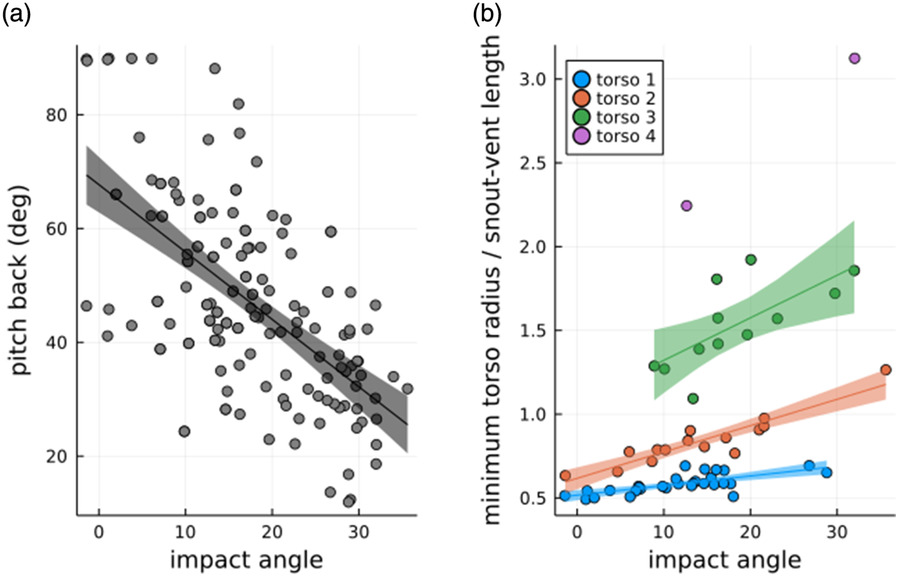
Figure 6
After the launch, the prototype experienced a slight roll or yaw during the glide in some experimental trials. The prototypes with torso stiffness S1torso and S2torso were able to accommodate the slight rolling at the time of impact and successfully perch due to the compliance. However, slight yaw or roll during the glide would make the perching fail in prototypes with torso stiffness S3torso and S4torso.
During arboreal locomotion, geckos have to land on vertical trees with irregular curvature after their aerial descent. Due to their limited aerodynamic control capabilities, precise control of their approach kinematics might not be possible, especially during a sudden escape response. The compliance in the torso might help geckos to account for surface variability of the landing area and aid perching successfully.
Approaching a target position for aerial robots is a complex task involving a feedback control architecture with sensors mounted onto the robot. Even with feedback control, it is difficult to accomplish this task due to the limited predictability of the unsteady disturbances (e.g., wind gusts) from the sensors. Hence, robots might not be able to land and perch precisely in the desired position. A compliant perching mechanism inspired by geckos can handle the variability and complexity of the surface texture and unpredictability of the approach kinematics via morphological intelligence. This potential helps robots to approach the target area with reduced control effort.
3 Conclusion
Mechanically mediated landing maneuvers with passive perching mechanisms can broaden the range of locomotion capabilities in arboreal and aerial robots with minimum additional components and control effort. The Asian flat-tailed gecko (H. platyurus) serves as a model system for the creation of such mechanisms. Their rapid FAR during perching after aerial descent motivated us to explore the role of their morphology on their perching strategy, by employing physical prototypes. Our analysis of tail stiffness, tail length, and torso stiffness shows that a long and high stiffness tail, combined with a low stiffness torso, low stiffness torso can produce robust perching behavior. The results underpin the importance of morphology in the transitions of locomotion, notably perching, in animals as well as robotic platforms. Geckos are able to perform complex air–land transitions even without highly evolved aerodynamic profiles. This study sheds light on the strategies that must be adopted to build a successful perching mechanism for multimodal robots capable of land–air transitions. Further developing the prototype to actively change the stiffness by close loop control can enhance the perching capabilities. Overall, through this comparative analysis we provide new insight on capabilities associated with hard landings and provide insights for novel perching mechanisms for aerial vehicles to successfully perch on challenging vertical substrates using mechanical integration that can increase stability and simplify control of perching.
4 Experimental Section
Experimental Setup and Data Collection
The prototype was launched to the vertical wall using a catapult. The catapult propelled a carriage along a linear guide rail with recirculating ball bearings toward a rubber stopper using stretched elastic (8 mm diameter, 1 mm-thick latex tubes). The carriage was retracted, tensioning the elastic, and then released, the release point being adjustable in increments of 20 mm. An electromagnet was used to secure the prototype to the carriage prior to and during launch. A trigger switch located 1 cm from the end of the rail deactivated the electromagnet, releasing the prototype without being harmed by the carriage’s impact with the stopper (Figure 7a, from Ref. 36, modified). The rig’s position can be changed to adjust the approach angle, and a digital inclinometer was attached to the linear rail to ensure orientation accuracy to within 0.1°. Between launch and landing, the aerial phase resulted in a change in the prototype’s angle and speed at impact. The landing surface consisted of an 8 mm-thick wooden plate covered in a sheet of felt fabric.
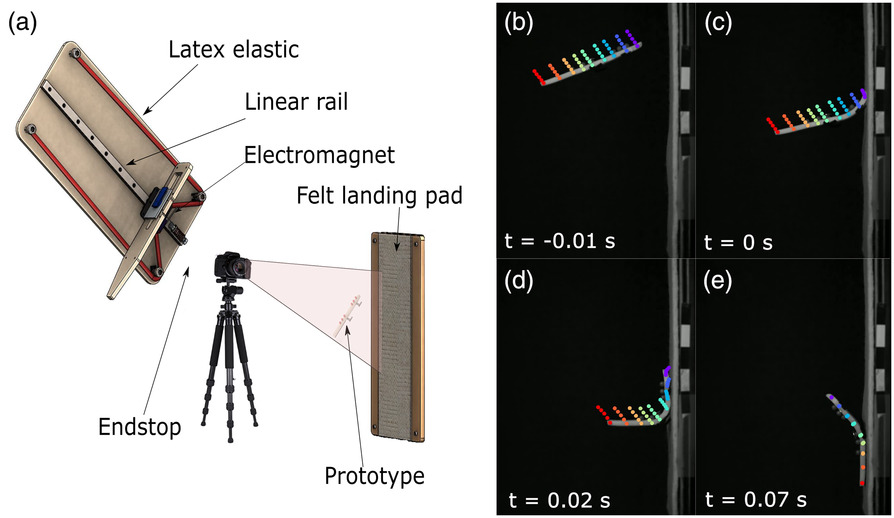
Figure 7
We performed 30 trials for each of the four different configurations—varying tail stiffness, body stiffness, and tail length. The FAR happens in a series of chronological events, as shown in Figure 1: 1) first impact with the head followed by the bending of the torso; 2) impact with the hind limbs; 3) impact with the tail; 4) pitch back of torso; and 5) forelimbs regain contact.
The FAR could fail in any of these steps. The stiffness of the torso and the tail play significant roles during these steps. Furthermore, for the FAR to transition from step 1 to step 2, the torso stiffness is of primary importance because if the torso does not bend at impact and absorb some amount of impact energy, the hindlimbs will not engage with the substrate and the physical model will fail to perch. Hence, to understand the role of either tail or torso stiffness, we initially ensured that the torso stiffness was appropriate to transition from step 1 to step 2, and then later experimented with different torso stiffnesses after optimizing the tail length and stiffness. Furthermore, the selection of initial torso stiffness was carried out within the constraints of the physical model closely matching the average dimensions of the gecko found in the wild. Overall, by following this rationale, we ensured that the physical model could elicit all five steps of the FAR which led us to choosing stiffness S1 for the torso. Hence, with torso stiffness (S1), we performed first set of experiments with different tail stiffness. Further, using the tail stiffness with the highest success rate, we performed the second set of experiments where the length was varied (tail lengths of 100%, 50%, and 0%). Using the tail stiffness and tail length with the highest success rate, we performed the third set of experiments in which we experimented with different torso stiffness.
Trials were recorded at 1000 frames per second using a single high-speed camera (S-Motion, AOS Technologies, Switzerland) set up perpendicular to and focused on the landing area. The high-speed camera was positioned orthogonal to the experimental setup and was leveled using an inclinometer to align the picture coordinate system with the vertical wall.
Data Processing
Automated tracking of multiple body points along the side of the prototype from the recorded video data was performed using the deep learning pose estimation package DeepLabCut.[38] A Resnet 50 deep learning network was trained on 200 images of the prototype covering various glide and perching configurations covering all four experimental setups. The network was trained for 950 000 iterations and was able to consistently track the high-contrast marking along the side of the prototype’s body. A total of nine points were tracked for experiments on varying tail stiffness, body stiffness, and the mass distribution. The half-tail prototype data consisted of seven tracked points and the no tail prototype data consisted of five tracked points.
The tracking output from the DeepLabCut package consisted of the pixel coordinates of the marked body points along with their tracking likelihood. The tracked pixel coordinates were filtered based on a tracking likelihood threshold of 0.98. The resultant pixel coordinates were calibrated against the dimensions of the prototype for each individual trial to obtain the XY coordinates. The calibrated trials were checked for consistency by calculating the length and comparing it with the actual measured length of the prototype. The variation in the calculated prototype length relative to the measured length was 98.1 ± 2.5% (N = 297) across all experimental trials. Postcalibration, each track was smoothed using a smoothing quintic spline followed by taking the first and second derivatives of the smoothed tracks to calculate the 2D velocity and acceleration. Each track was translated to make the point of impact of the anterior part of the prototype with the vertical landing surface as X = 0 m at time, t = 0 s.
Data Analysis
The following kinematic variables were calculated to analyze the kinematics of perching (Figure 8):
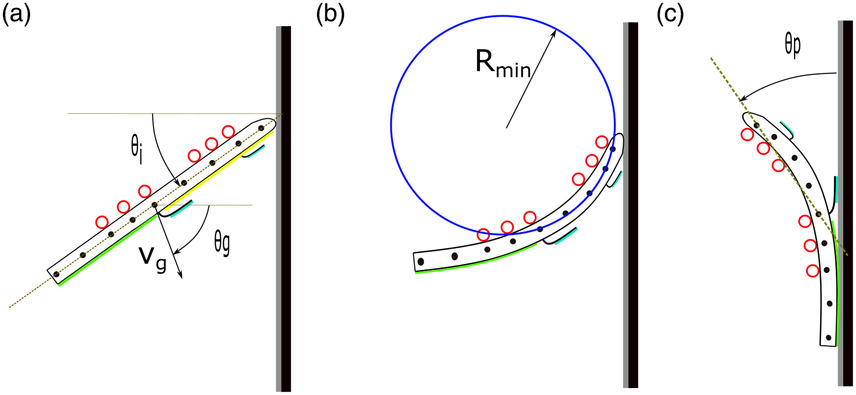
Figure 8
Prototype Orientation (θo)
The angle made by a line joining the anterior most and posterior most tracked points with the horizontal. The prototype orientation at impact is denoted by �oi.
Glide Angle (θg)
The angle defined by the inverse tangent of the ratio of the vertical component of velocity to the horizontal component of glide velocity (�g). Glide angle at impact is denoted by �gi.
Pitch Back Angle (θP)
The orientation of torso with respect to Y-axis after the rebound of the anterior body with hind limbs in contact. The orientation is measured as the angle between line joining markers 1 and 5 with respect to the vertical axis.
Minimum Radius of Torso Curvature (Rmin)
The minimum radius of the circle formed by the markers 1, 3, and 5 (numbered in order from head to tail) during the bending of the torso from the time of collision with the head to the impact of the hind limbs. The extend of torso bending was evaluated by the ratio of �min and snout-vent length (�sv).
Analysis and Statistical Methods
All analyses were performed in MATLAB 2021b (The MathWorks, Natick, MA, USA) using custom written scripts. The average metrics reported follow the format of (mean ± SD), unless otherwise stated.
Acknowledgements
The authors thank the Max Planck Society and Cyber Valley for funding this research (grants to A.J., Nr. CyVy-RF-08-2019). The authors thank the Max Planck Institute for Intelligent Systems Central Service Station for Robotics for additive manufacturing support. A.J. is most grateful to Hyrzeme Sefa-Jusufi. The authors thank Gregory Byrnes for valuable insights. The authors thank Metin Sitti for access to an Instron Materials Tester.

